どうも！KAZUTOです！
↓↓さらに飛躍したい君に↓↓
Contents
三角関数の覚え方
3つの
三角関数の覚え方
から紹介していきます。
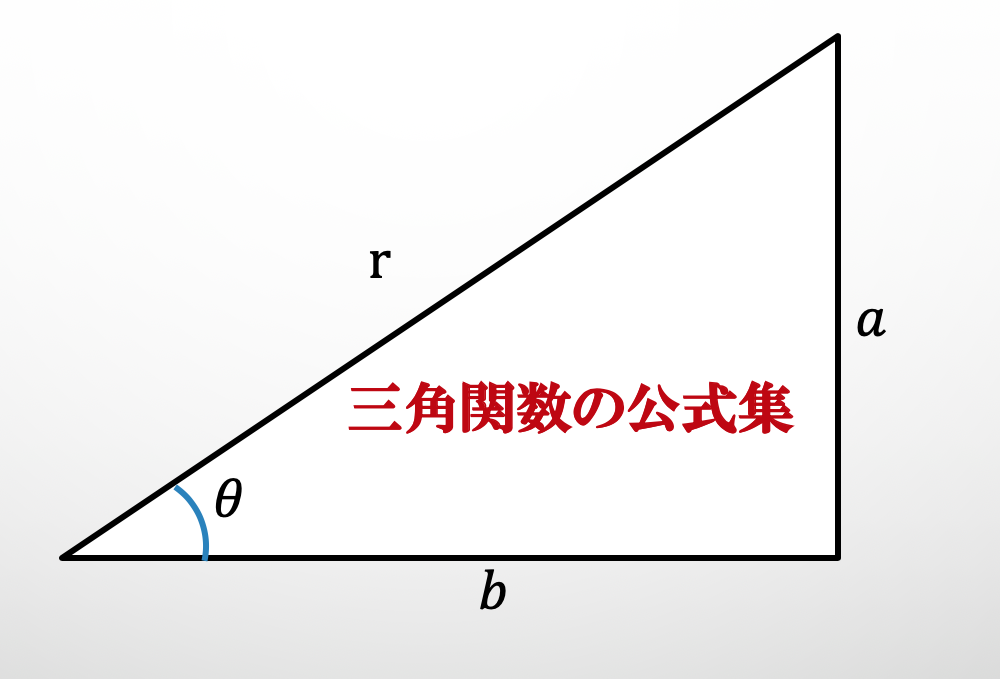
この時以下のような三角形を考えます。 
そして、左から右に線を引いてあげます。
この時線がまたいでいる2本の辺を使い、
最初に通過した辺を分母に
次に通過した辺を分子におき
次のようにして$\sin$が定義されます。
$$ \Large \sin \theta = \frac {a}{r}$$
次に上から下へ線を引いてあげます。
この時線がまたいでいる2本の辺を使い、
最初に通過した辺を分母に
次に通過した辺を分子におき
次のようにして$\cos$が定義されます。
$$ \Large \cos \theta = \frac {b}{r}$$
最後に左下から右上に向かって線を引いてあげます。
この時線がまたいでいる2本の辺を使い、
最初に通過した辺を分母に
次に通過した辺を分子におき
次のようにして定義されます。
$$ \Large\tan \theta = \frac {a}{b}$$
これら三角関数の
基本公式としては
$$\Large \sin^{2}\theta + \cos^{2}\theta=1$$
$$\Large 1+\tan^{2}\theta=\frac{1}{\cos^{2}\theta}$$
があります。
1つ目の公式は三角関数の定義から、
2つ目の式は1つ目の公式から導かれます。
加法定理
\begin{align}& \Large \sin (\alpha \pm \beta) \\
\\&\Large= \sin \alpha \cos \beta \pm \cos \alpha \sin \beta
\\
\\
\\
\\
&\Large \cos (\alpha \pm \beta) \\
\\& \Large= \cos \alpha \cos \beta \mp \sin \beta \sin \alpha
\\
\\
\\
\\
&\Large \tan (\alpha \pm \beta) \\
\\ &\Large= \frac{\tan \alpha \pm \tan \beta}{1-\mp \tan \alpha \tan \beta}\end{align}
$ \sin (\alpha+\beta)$に関しては
咲いたコスモス コスモス咲いた
$ \cos (\alpha+\beta)$に関しては
コスモスコスモス 咲いた咲いた
という覚え方があるので利用してみると良いです。
この公式はもちろん導出できるものですが、
覚えてしまった方が簡単なので導出までしっかり理解しておく必要はあまりないです。
倍角の公式
\begin{eqnarray} \Large \sin 2\theta &\Large=& \Large 2\sin \theta \cos \theta
\\
\\
\\
\Large \cos 2\theta &\Large=& \Large \cos^{2}\theta-\sin^{2}\theta
\\
\\
&\Large=& \Large 2\cos^{2}\theta -1
\\
\\
&\Large=& \Large 1-2 \sin^{2}\theta
\\
\\
\\
\Large \tan 2\theta &\Large=& \Large \frac{2\tan\theta}{1- \tan^{2}\theta}\end{eqnarray}
これらは加法定理から
導くことができます。
$ \cos 2\theta $について
どの変形を使うかは
適宜自分で判断するようにして下さい。
基本的に三角関数の問題ではsinかcosの
どちらか一方だけが
出てくる式にして考える
というのが基本なので、これを念頭におけば
どの変形を使うべきかも見通しがつきやすいです。
半角の公式
\begin{eqnarray} \Large \sin^{2} \frac{\theta}{2} &\Large=& \Large \frac{1-\cos2\theta}{2}
\\
\\
\\
\\
\Large \cos^{2} \frac{\theta}{2} &\Large=& \Large \frac{1+\cos2\theta}{2}\end{eqnarray}
これらは倍角の公式から
導くことができます。
正弦定理
正弦定理とは以下のように
半径$R$の円に内接する
次のような三角形について
$$\Large \frac{A}{\sin \alpha }= \frac{B}{\sin \beta}= \frac{C}{\sin \gamma}=2R$$
が成り立つことを指します。
余弦定理
余弦定理では以下のような三角形に対して
$$\Large a^2=b^2+c^2-2bc\cos \theta$$
が成り立つことを指します。
和積の公式
\begin{align} & \Large \sin \alpha + \sin \beta \\
&\Large = 2\sin{\frac{\alpha + \beta}{2}}\cos{\frac{\alpha – \beta}{2}}
\\
\\
\\
& \Large \sin \alpha – \sin \beta \\
&\Large = 2\sin{\frac{\alpha – \beta}{2}}\cos{\frac{\alpha + \beta}{2}}
\\
\\
\\
&\Large \cos \alpha + \cos \beta \\
&\Large = 2\cos{\frac{\alpha + \beta}{2}}\cos{\frac{\alpha – \beta}{2}}
\\
\\
\\
&\Large \cos \alpha – \cos \beta \Large \\
& \Large = -2\sin{\frac{\alpha + \beta}{2}}\sin{\frac{\alpha – \beta}{2}} \end{align}
これらは加法定理で得られた
それぞれの式を連立することで導出できます。
積和の公式
\begin{align}
&\Large \sin \alpha \cos \beta \\
& \Large = \frac{1}{2}\{ \sin(\alpha+\beta)+\sin(\alpha-\beta)\}
\\
\\
\\
&\Large \sin \alpha \sin \beta \\
&\Large = -\frac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}
\\
\\
\\
&\Large \cos \alpha \cos \beta \\
&\Large = \frac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\}\end{align}
これらは和積の公式を
用いて導出できます。
3倍角の公式
\begin{eqnarray} \Large \sin 3\theta &\Large =& \Large 3\sin \theta-4\sin^{3}\theta
\\
\\
\\
\Large \cos 3\theta &\Large=& \Large 4\cos^{3}\theta-3\cos \theta
\end{eqnarray}
これらは加法定理を用いて導出できます。
以上が
三角関数に関する公式
になります！
これらの存在をしっかりと意識し
問題に取り組む際
すぐに使えるようにしておきましょう！
あと、左から右に公式を読んだろうが
問題によっては紹介した公式を
右から左に使う場合もあるので
そのことも頭に入れておいてな！
今回はこれで以上だ！
↓↓さらに飛躍したい君に↓↓
今回は
三角関数の公式
を一挙紹介していきます！