どうも!KAZUTOです!

今回導出する公式は以下の2つの公式です。
\begin{eqnarray} \Large \sin^{2} \frac{\theta}{2} &\Large=& \Large \frac{1-\cos2\theta}{2}
\\
\\
\\
\\
\Large \cos^{2} \frac{\theta}{2} &\Large=& \Large \frac{1+\cos2\theta}{2}\end{eqnarray}
Contents
\begin{eqnarray} \Large \sin^{2} \frac{\theta}{2} &\Large=& \Large \frac{1-\cos2\theta}{2}\end{eqnarray}
ここでは
$$\Large \cos 2\theta = 1-2\sin^{2}\theta \tag{1}$$
で表される倍角の公式を使います。
この(1)を変形すると
$$\Large \sin^{2}\theta = \frac{1-\cos2\theta}{2} \tag{2}$$
が得られます。
もうわかりましたね?
この(2)式において$\theta → \frac{\theta}{2}$
というように書き換えると
$$ \Large \sin^{2} \frac{\theta}{2} = \frac{1-\cos2\theta}{2}$$
という半角の公式が得られます。
\begin{eqnarray}\Large \cos^{2} \frac{\theta}{2} = \frac{1+\cos2\theta}{2}\end{eqnarray}
では次です。
ここでは
$$\Large \cos 2\theta = 2\cos^{2}\theta-1 \tag{3}$$
という先ほどとは別の
倍角の公式を用います。
この(3)を変形すると
$$\Large \cos^{2}\theta = \frac{1+\cos2\theta}{2} \tag{4}$$
が得られます。
この(4)式において先程のように$\theta → \frac{\theta}{2}$
というように変換を行うと
\begin{eqnarray}\Large \cos^{2} \frac{\theta}{2} = \frac{1+\cos2\theta}{2}\end{eqnarray}
という求めたい
半角の公式を得ることができます。
以上が半角の公式の導出です。
半角の公式の使い所
半角の公式はどんな時に使われるか
についてです。

半角の公式は主に
三角関数の次数を
下げたい場合
に用いられます。
ここで字数とは
三角関数の肩に乗っている数字のことです。
この公式の利点は
次数を2から1に
下げることができる
という点にあります。
次数を下げた方がいいかどうかは
適宜自分で判断するしかありませんが、
とにかく
半角の公式は
三角関数の次数を
下げることができる
という点は覚えておきましょう。

半角の公式を丸暗記する必要はなくなるので
今回解説した内容は
しっかりと理解しておくようにな!
あとこの公式の利点も
しっかり覚えておくように!
今回はこれで以上だ!
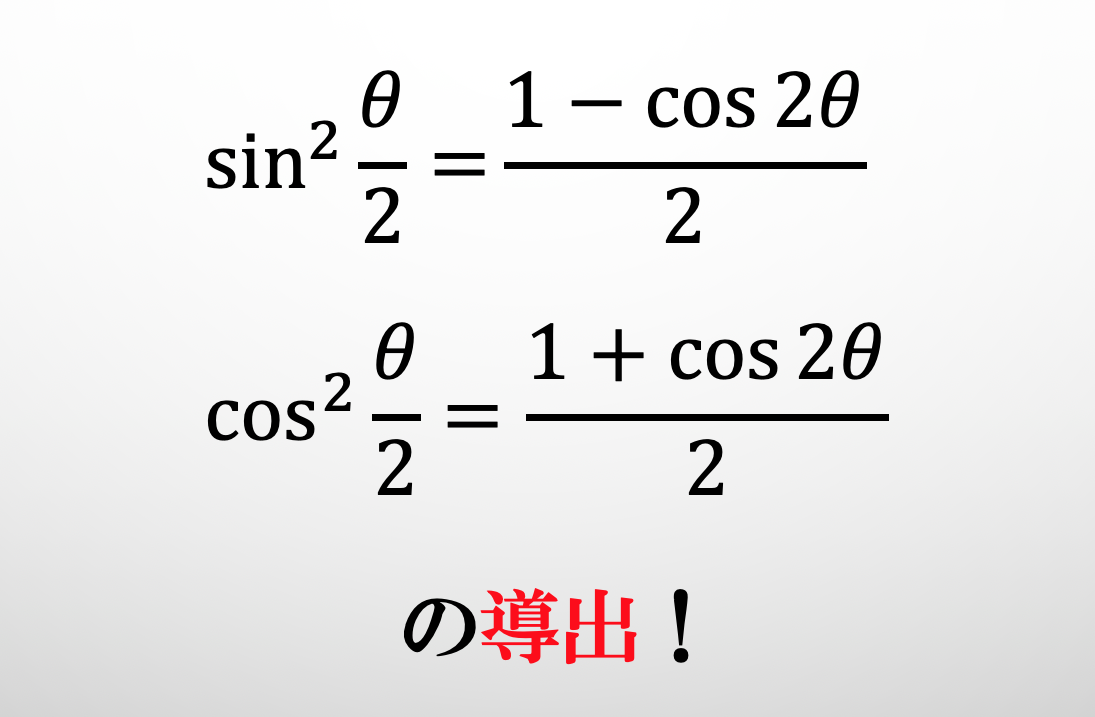











今回は
半角の定理の導出
を解説していきます!