どうも！KAZUTOです！
Contents
$\sin^{2} \theta+\cos^{2} \theta=1の導出$
まず以下のような単位円を考えます。
単位円とは半径が１の円のことです。
つまりこの円において
円上の全ての点について
その点と原点を繋いだ線分の長さは１になります。
そしてその性質と三角関数の定義から
以下のように$\Large \theta$を定めると
円上の各点の座標は
$$\Large x=\cos \theta$$
$$\Large y=\sin \theta $$
このように表すことができます。
座標$(x,y)$と減点と距離$\large r$には
３平方の定理より
$$\Large x^2+y^2=r^2$$
という関係が成り立つことから、
この時円の半径は1
つまり$\Large r=1$なので
これらを代入して
$$ \Large \sin^{2} \theta+\cos^{2} \theta=1$$
が導かれます。
$1+\tan^{2}\theta =\frac{1}{\cos^{2}\theta}の導出$
これは
$$ \Large \sin^{2} \theta+\cos^{2} \theta=1$$
を愚直に式変形していくことで得られます。
$$ \Large \sin^{2} \theta+\cos^{2} \theta=1$$
の両辺をまず$\cos^{2} \theta$で割ります。
すると
$$ \Large \frac{\sin^{2} \theta}{\cos^{2} \theta}+1=\frac{1}{\cos^{2} \theta}$$
また
$$ \Large \tan \theta=\frac{\sin \theta}{\cos \theta}$$
なので、これを使って
上の式は
$$ \Large \tan^{2} \theta +1=\frac{1}{\cos^{2} \theta}$$
つまり
$$\Large 1+\tan^{2}\theta =\frac{1}{\cos^{2}\theta}$$
を導くことができました。
以上が三角関数の基本公式の導出になります！
これらの導出過程を知っていれば
その場で自分で公式を作り出せて
丸暗記する必要はなくなるからちゃんと理解しておくように！
今回はこれで以上だ！
↓↓さらに飛躍したい君に↓↓
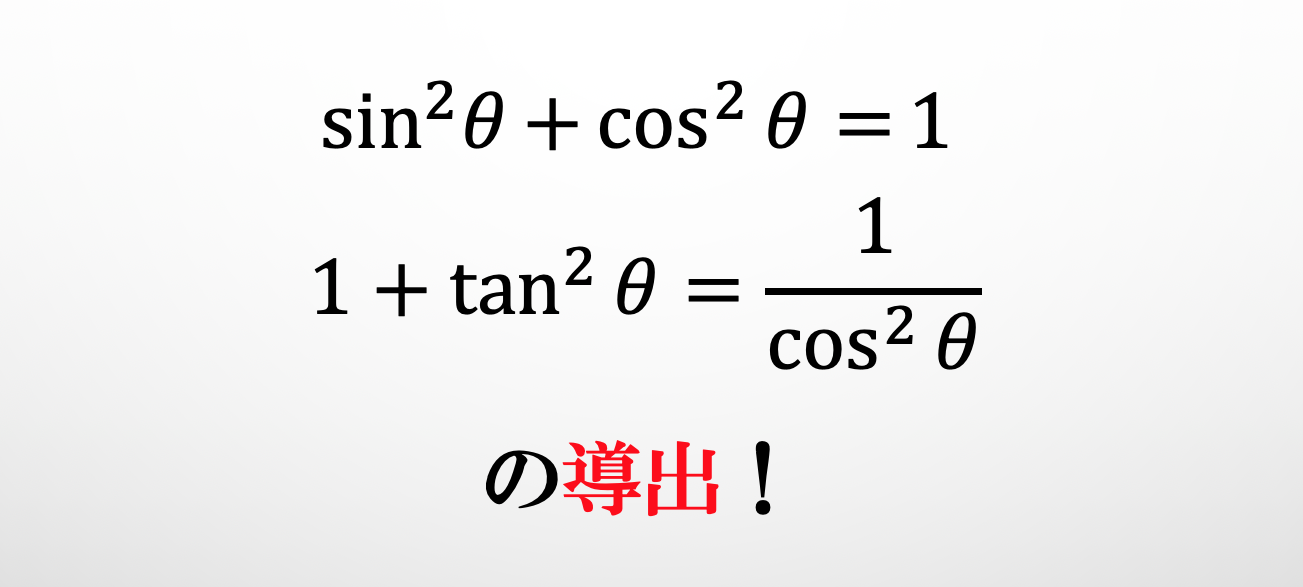
今回は
三角関数の
基本公式の導出
を解説していきます！